非確定有限自動機
NFA (Nondeterministic Finite Autoaumata)
NFA定義
跟DFA差別只在於原本每次轉移都能決定唯一的狀態,但NFA不能決定(Nondeterministic),他的狀態轉移是一個集合.白話講就是一個輸入可以得到好幾個狀態.
δ(q, w) = {qk, qk+1, qk+2,...}
NFA數學定義
An NFA is represented formally by a 5-tuple, (Q, Σ, Δ, q0, F), consisting of
a finite set of states Q a finite set of input symbols Σ a transition function Δ : Q × Σ → P(Q). an initial (or start) state q0 ∈ Q a set of states F distinguished as accepting (or final) states F ⊆ Q. Here, P(Q) denotes the power set of Q. Let w = a1a2 ... an be a word over the alphabet Σ. The automaton M accepts the word w if a sequence of states, r0,r1, ..., rn, exists in Q with the following conditions:
r0 = q0 ri+1 ∈ Δ(ri, ai+1), for i = 0, ..., n−1 rn ∈ F.
狀態圖
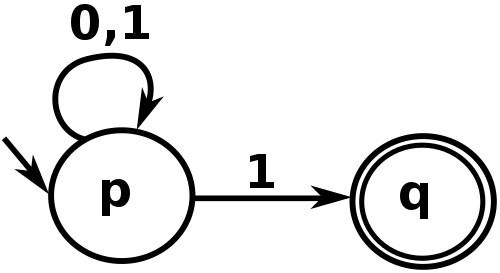
ε-NFA定義
就是擴展NFA,原本DFA有一個起始狀態q0,但假設有好幾個狀態q(ε),都是起始狀態不用輸入就可以轉換過去的,那這種NFA就叫做ε-NFA.
ε-NFA數學定義
An NFA-ε is represented formally by an 5-tuple, (Q, Σ, Δ, q0, F), consisting of
a finite set of states Q a finite set of input symbols called the alphabet Σ a transition function Δ : Q × (Σ ∪ {ε}) → P(Q) an initial (or start) state q0 ∈ Q a set of states F distinguished as accepting (or final) states F ⊆ Q. Here, P(Q) denotes the power set of Q and ε denotes empty string.
For a q ∈ Q, let E(q) denote the set of states that are reachable from state q by following ε-transitions in the transition function Δ, i.e., p ∈ E(q) iff there is a sequence of states q1,..., qk such that
q1 = q, qi+1 ∈ Δ(qi, ε) for each 1 ≤ i < k, and qk = p. E(q) is known as the ε-closure of q.
ε-closure is also defined for a set of states. The ε-closure of a set of states, P, of an NFA is defined as the set of states reachable from any state in P following ε-transitions. Formally, for P ⊆ Q, E(P) = ∪q∈P E(q).
Let w = a1a2 ... an be a word over the alphabet Σ. The automaton M accepts the word w if a sequence of states, r0,r1, ..., rn, exists in Q with the following conditions:
r0 ∈ E(q0), ri+1 ∈ E(r') where r' ∈ Δ(ri, ai+1) for each i = 0, ..., n−1, and rn ∈ F.
狀態圖

狀態轉移列表
跟DFA大同小異只是他右邊的輸出狀態比較多,如果是ε-NFA則輸入項多一個ε.
例如
| Input/State | 0 | 1 | ε |
|---|---|---|---|
| S0 | {} | {} | {S1, S3} |
| S1 | {S2} | {S1} | {} |
| S2 | {S1} | {S2} | {} |
| S3 | {S3} | {S4} | {} |
| S4 | {S4} | {S3} | {} |
可以看出來其實就是多一個輸入ε的列表